Hoy os voy a explicar cómo calcular una recta paralela a dos planos. Este problema es el mismo que el de buscar una recta paralela a otra recta. Lo único diferente es que en este problema no tenemos la recta sino los dos planos que “formarían” esta recta.
Tenemos que hallar la rectar paralela a dos planos que pase por el punto P. Sean estos los datos:

Cómo podíais ver en la imagen, dos planos al cortarse forman una recta, por lo tanto lo que buscamos realmente es la recta paralela a esta recta que forman.

Una recta queda definida por un punto y un vector director. El punto nos lo dan en el enunciado. Y el vector, al ser una recta paralela, será el mismo que el de la recta que forman los dos planos.
Hay muchas maneras de calcular el vector director de la recta que forman estos dos planos. El método que me parece más sencillo si los planos están en forma general es hacer el producto vectorial de sus vectores normales.
Como podéis ver en la imagen, el vector director de la recta es perpendicular a los dos vectores normales, por eso, al hacer el producto vectorial tendremos el vector director.

Además, si tenemos los planos en ecuación general, los vectores normales se ven fácilmente, ya que recordemos que si:
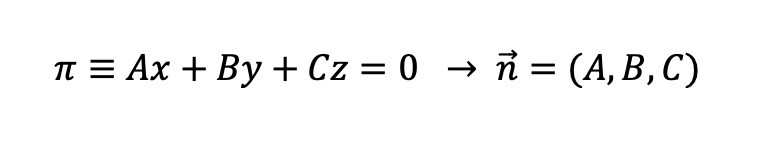
Por lo tanto, los vectores normales de los dos planos y su correspondiente producto vectorial será:
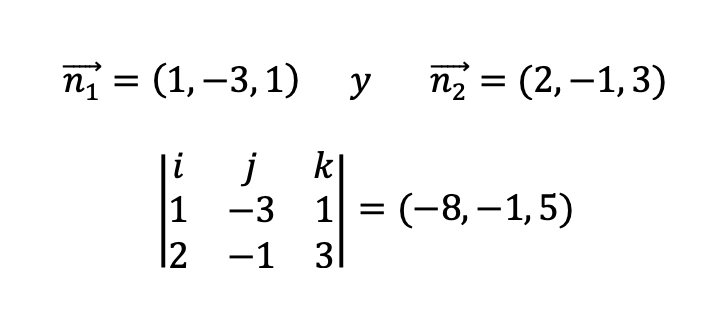
Ahora ya tenemos el vector director de la recta que forman los planos que, como son paralelas, será el mismo que el de la recta que buscamos. Por lo tanto, con el punto y el vector ya podemos poner la ecuación de la recta en forma vectorial.
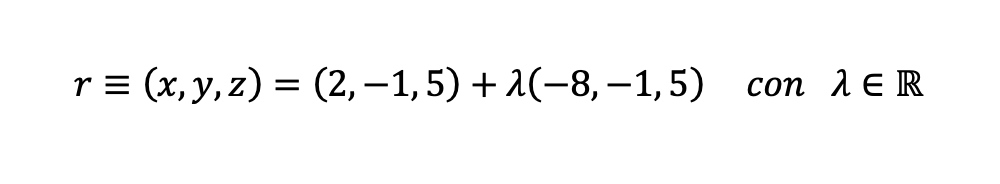
El problema ya estaría acabado, pero como las ecuaciones de los planos nos las han dado en forma general, siempre recomiendo a mis alumnos dar la respuesta con el mismo tipo de ecuación que el enunciado. Por lo tanto, vamos a pasar la ecuación vectorial de la recta a su ecuación general.
La mejor forma es pasándolo primero a la ecuación continua y de ahí sacar las dos igualdades. Recordamos las fórmulas:

Entonces en nuestro caso quedaría:
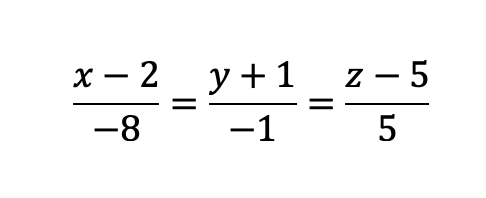
De aquí sacamos dos ecuaciones igualando, por ejemplo, las dos primeras fracciones y las dos últimas (también podríamos haber cogido la primera con la tercera), las despejamos y nos quedan las dos ecuaciones de la recta.

Y ya tenemos la solución con la recta en forma general, acabando así el problema.
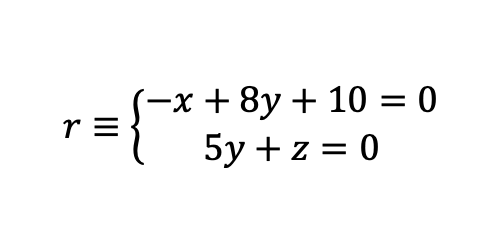
Video de la recta paralela a dos planos
A continuación tenéis el video explicativo de la recta paralela a dos planos enseñando paso por paso cómo se soluciona. Podéis pausar y repetir el video las veces que queráis.
Quizás te pueda interesar un tema que hice hace no mucho y es la recta perpendicular a un plano. Si tenéis cualquier duda o sugerencia podéis usar las redes sociales para estar en contacto. Por ejemplo me podéis encontrar en twitter o instagram.
